
Penyelesaian Persamaan garis Lurus
Dua persamaan ini dapat direpresentasikan bersama sebagai suatu sistem persamaan linear dengan dua variabel dan memiliki bentuk:
ax + by = cdx + ey = f
Dilambangkan dengan x dan y sebagai variabel atau peubah. Sedangkan huruf a,b,d,e merupakan suatu koefisien. Kemudian huruf c dan f merupakan sebuah konstanta.
Ada dua cara untuk menyelesaikan sistem persamaan dua variabel, yaitu metode substitusi dan metode eliminasi. Penjelasan berikut:
1. Metode Substitusi
Dalam metode substitusi, salah satu variabel harus dipisahkan dari persamaan tersebut. Bentuk persamaannya adalah berbentuk ax + by = c diubah sehingga memiliki bentuk eksplisit:

Persamaan hasil substitusi memiliki 1 variabel sehingga dapat diselesaikan.
2. Metode Eliminasi
Dalam metode eliminasi, salah satu variabel dieliminasi dengan mengurangi dua persamaan yang ada. Agar variabel dapat dihilangkan ketika dua persamaan dikurangi, koefisien dari kedua variabel tersebut pertama kali disamakan. Persamaan koefisien ini dengan mengalikan atau membagi persamaan dengan angka. Jadi ini:
ax + by = c | xp
dx + ey = f | x1
dengan
a x p = d
Dan persamaannya menjadi:
(ap)x + (bp)y = (cp)
dx + ey = f
Kemudian dapat kita eliminasi dengan cara mengurangi persamaan pertama dengan persamaan kedua :
(ap)x+(bp)y=(cp)
dx + ey = f
___________________-
(bp-e)y = cp-f
Sehingga hasil penyelesaiannya akan didapat menjadi:
y = (cp-f) / (bp-e)
Nilai variabel y yang diketahui dapat dimasukkan ke dalam persamaan untuk mendapatkan nilai variabel x.
Gradien Persamaan Garis Lurus
Gradien menunjukkan kemiringan suatu persamaan sehubungan dengan garis x. Ini ditandai dengan huruf m. Berdasarkan gambar berikut:
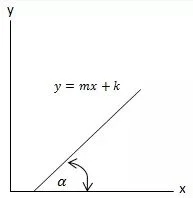 1px 1px 1px;) Gradien = m = tan α
Gradien = m = tan α
Untuk beberapa bentuk persamaan, gradien diperoleh dengan:

Contoh Soal :
Tiga garis A, B, C memiliki gradien masing-masing 3, 4, 5. Ketiga garis memotong sumbu y di titik yang sama. Jika absis masing-masing garis ke sumbu x di jumlahkan hasilnya adalah 47/60, tentukan persamaan garis A.
Pembahasan:
Diketahui persamaan masing-masing garis:
A -> y = 3x + CA
B -> y = 4x + CB
C -> y = 5x + CC
Karena memotong sumbu y di yang sama, maka
CA = CB = CC. Selanjutnya disebut C.
Absis (saat y=0) masing-masing garis adalah:
A -> 0 = 3x + C -> x1 = -C/3
B -> 0 = 4x + C -> x2 = -C/4
C -> 0 = 5x + C -> x3 = -C/5
Ketiga absis dijumlahkan:
x1 + x2 + x3 = 47/60
-C/3 – C/4 – C/5 = 47/60
-47C/60 = 47/60
C = -1
Sehingga:
A -> y = 3x – 1
Demikian penjelasan tentang Materi Matematika Kelas 10 – Persamaan Garis kali ini, semoga bermanfaat bagi anda.